Atšķirība starp korelāciju un regresiju ir viens no visbiežāk uzdotajiem jautājumiem intervijās. Turklāt daudzi cilvēki cieš neskaidrības par šo divu izpratni. Tātad, pilnībā izlasiet šo rakstu, lai iegūtu skaidru izpratni par šiem diviem.
Salīdzinājuma diagramma
| Salīdzinājuma pamats | Korelācija | Regresija |
|---|---|---|
| Nozīme | Korelācija ir statistisks pasākums, kas nosaka divu mainīgo savstarpējo attiecību vai asociāciju. | Regresija apraksta, kā neatkarīgs mainīgais ir skaitliski saistīts ar atkarīgo mainīgo. |
| Lietošana | Lai attēlotu lineāro attiecību starp diviem mainīgajiem. | Lai uzstādītu labāko līniju un novērtētu vienu mainīgo, pamatojoties uz citu mainīgo. |
| Atkarīgie un neatkarīgie mainīgie | Nav atšķirības | Abi mainīgie ir atšķirīgi. |
| Norāda | Korelācijas koeficients norāda, cik lielā mērā divi mainīgie kustas kopā. | Regresija norāda uz vienības izmaiņu ietekmi uz zināmo mainīgo (x) uz aplēsto mainīgo (y). |
| Mērķis | Atrast skaitlisku vērtību, kas izsaka attiecības starp mainīgajiem. | Novērtēt nejauša mainīgā lieluma vērtības, pamatojoties uz fiksētā mainīgā lieluma vērtībām. |
Korelācijas definīcija
Termins "korelācija" ir divu vārdu kombinācija "Co" (kopā) un attiecības (savienojums) starp diviem daudzumiem. Korelācija ir tad, kad divu mainīgo lielumu izpētes laikā tiek konstatēts, ka vienības mainība vienā mainīgajā lielumā ir atkal saistīta ar citu mainīgo, ti, tiešu vai netiešu. Vai arī tiek uzskatīts, ka mainīgie nav korelēti, ja kustība vienā mainīgajā lielumā nav nekāda kustība citā mainīgā lielumā noteiktā virzienā. Tā ir statistikas metode, kas attēlo mainīgo lielumu savienojuma stiprumu.
Korelācija var būt pozitīva vai negatīva. Ja abi mainīgie mainās vienā virzienā, ti, viena mainīgā pieaugums radīs atbilstošu palielinājumu citā mainīgajā lielumā un otrādi, tad mainīgie tiek uzskatīti par pozitīvi korelētiem. Piemēram : peļņa un ieguldījumi.
Gluži pretēji, ja abi mainīgie mainās dažādos virzienos, tādā veidā, ka viena mainīgā lieluma palielināšanās izraisīs cita mainīgā samazināšanos un otrādi, šī situācija ir pazīstama kā negatīva korelācija. Piemēram : produkta cena un pieprasījums.
Korelācijas pasākumi ir norādīti kā:
- Karl Pearson ražojuma momenta korelācijas koeficients
- Spearmana rangu korelācijas koeficients
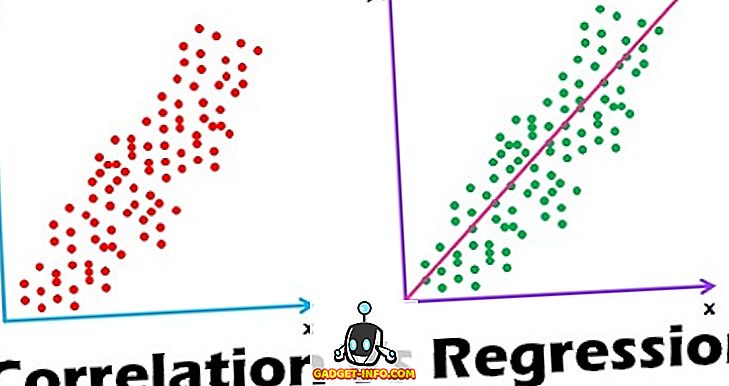
- Scatter diagramma
- Vienlaicīgu noviržu koeficients
Regresijas definīcija
Statistiskā metode, lai novērtētu mainīgo metriskā mainīgā lieluma izmaiņas vienas vai vairāku neatkarīgu mainīgo izmaiņu dēļ, pamatojoties uz vidējo matemātisko attiecību starp diviem vai vairākiem mainīgajiem lielumiem, ir pazīstama kā regresija. Tam ir nozīmīga loma daudzās cilvēka aktivitātēs, jo tas ir spēcīgs un elastīgs instruments, kas izmantoja, lai prognozētu pagātnes, tagadnes vai nākotnes notikumus, pamatojoties uz iepriekšējiem vai pašreizējiem notikumiem. Piemēram : Pamatojoties uz iepriekšējiem ierakstiem, var novērtēt uzņēmuma nākotnes peļņu.
Vienkāršā lineārā regresijā ir divi mainīgie x un y, kur y ir atkarīgs no x vai saka, ko ietekmē x. Šeit y tiek saukts par atkarīgu, vai kritērija mainīgais un x ir neatkarīgs vai paredzams mainīgais. Y regresijas līnija x tiek izteikta kā:
y = a + bx
kur, a = konstante,
b = regresijas koeficients,
Šajā vienādojumā a un b ir divi regresijas parametri.
Galvenās atšķirības starp korelāciju un regresiju
Turpmāk minētie punkti izskaidro atšķirību starp korelāciju un regresiju:
- Statistiskais pasākums, kas nosaka divu daudzumu kopsakarību vai asociāciju, ir pazīstams kā korelācija. Regresija apraksta, kā neatkarīgs mainīgais ir skaitliski saistīts ar atkarīgo mainīgo.
- Korelāciju izmanto, lai attēlotu lineāro attiecību starp diviem mainīgajiem. Gluži pretēji, regresiju izmanto, lai piemērotu labāko līniju un novērtētu vienu mainīgo, pamatojoties uz citu mainīgo.
- Korelācijā starp atkarīgajiem un neatkarīgajiem mainīgajiem nav atšķirības, ti, korelācija starp x un y ir līdzīga y un x. Un otrādi, y regresija uz x ir atšķirīga no x uz y.
- Korelācija norāda saistību starp mainīgajiem lielumiem. Atšķirībā no tā, regresija atspoguļo vienības maiņas ietekmi uz neatkarīgo mainīgo atkarīgajam mainīgajam.
- Korelācijas mērķis ir atrast skaitlisku vērtību, kas izsaka attiecības starp mainīgajiem. Atšķirībā no regresijas, kuras mērķis ir paredzēt nejauša mainīgā lielumus, pamatojoties uz fiksētā mainīgā lieluma vērtībām.
Secinājums
Ar iepriekš minēto diskusiju ir skaidrs, ka starp šīm divām matemātiskajām koncepcijām ir liela atšķirība, lai gan šīs divas ir pētītas kopā. Korelācija tiek izmantota, ja pētnieks vēlas zināt, vai pētāmie mainīgie ir savstarpēji saistīti vai nē, ja jā, tad kāda ir to asociācijas stiprība. Pearson korelācijas koeficients tiek uzskatīts par labāko korelācijas rādītāju. Regresijas analīzē tiek izveidota funkcionāla saikne starp diviem mainīgajiem lielumiem, lai nākotnē prognozētu notikumus.