Šķirošana ir pamatdarbība, kurā masīva elementi ir sakārtoti kādā konkrētā secībā, lai uzlabotu tā meklēšanu. Vienkārši runājot, dati ir sakārtoti tā, lai tos varētu viegli meklēt.
Salīdzinājuma diagramma
| Salīdzināšanas pamats | Ievietošanas kārtošana | Atlases kārtošana |
|---|---|---|
| Pamata | Dati tiek sakārtoti, ievietojot datus esošajā sakārtotajā failā. | Dati tiek sakārtoti, atlasot un novietojot secīgos elementus sakārtotā vietā. |
| Daba | Stabils | Nestabils |
| Process, kas jāievēro | Elementi ir zināmi jau iepriekš, bet atrašanās vieta, kur tos novietot, tiek meklēta. | Atrašanās vieta iepriekš ir zināma, kamēr tiek meklēti elementi. |
| Tūlītēji dati | Ievietošanas kārtība ir dzīva šķirošanas metode, kas var tikt galā ar tūlītējiem datiem. | Tā nevar risināt tūlītējus datus, tai jābūt klāt sākumā. |
| Labākais gadījuma sarežģītība | O (n) | O (n 2 ) |
Ievietošanas kārtošanas definīcija
Ievietošanas kārtošana darbojas, ievietojot vērtību kopu esošajā sakārtotajā failā. Tā veido sakārtotu masīvu, ievietojot vienu elementu vienlaicīgi. Šis process turpinās, līdz viss masīvs ir sakārtots kādā secībā. Galvenais aizlīmēšanas jēdziens ir ievietot katru vienumu atbilstošajā vietā galīgajā sarakstā. Ievietošanas kārtība ietaupa efektīvu atmiņas apjomu.
Ievietošanas kārtība
- Tajā tiek izmantoti divi bloku komplekti, kuros tiek glabāti sakārtotie dati un citi nešķirotiem datiem.
- Šķirošanas algoritms darbojas līdz brīdim, kad nesaglabātajā komplektā ir elementi.
- Pieņemsim, ka masīvā ir 'n' skaitļu elementi. Sākumā šķirotajā komplektā ir elements ar indeksu 0 (LB = 0). Atlikušie elementi ir saraksta nesadalītajā nodalījumā.
- Pirmā nešķirotās daļas elementam ir masīva indekss 1 (ja LB = 0).
- Pēc katras atkārtošanas tā izvēlas nesaistītā partition pirmo elementu un ievieto to pareizajā vietā šķirotajā komplektā.
Ievietošanas priekšrocības
- Viegli lietojama un ļoti efektīva, ja to izmanto ar maziem datu kopumiem.
- Papildu atmiņas vietas nepieciešamība ievietošanas kārtībā ir mazāka (ti, O (1)).
- To uzskata par dzīvu šķirošanas tehniku, jo sarakstu var sakārtot, saņemot jaunos elementus.
- Tas ir ātrāks nekā citi šķirošanas algoritmi.
Piemērs :
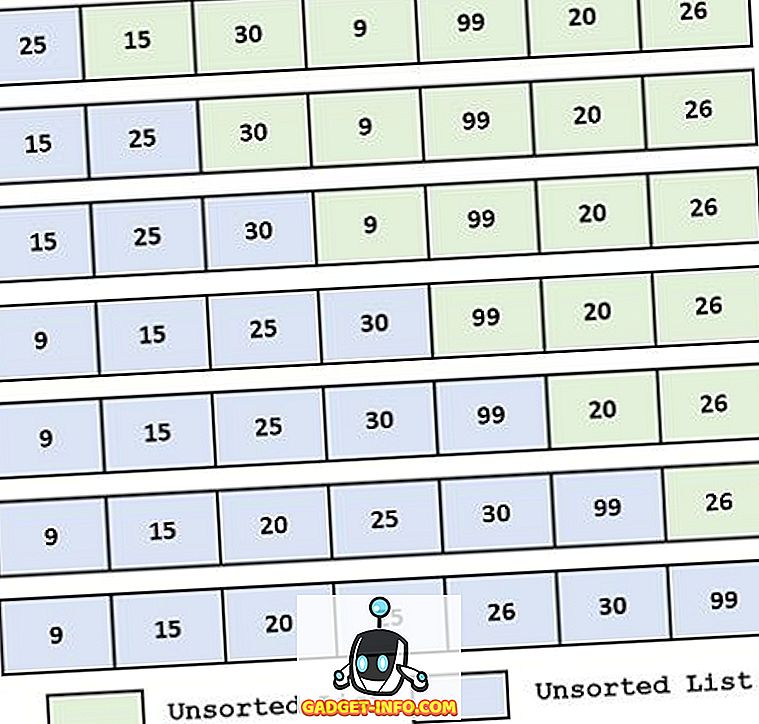
Atlases definīcija Kārtot
Atlases kārtība veic šķirošanu, meklējot minimālo vērtību skaitu un ievietojot to pirmajā vai pēdējā pozīcijā pēc pasūtījuma (augošā vai dilstošā secībā). Tiek turpināts minimālās atslēgas meklēšanas un pareizas novietošanas process, līdz visi elementi atrodas pareizajā pozīcijā.
Atlases rīkošana
- Pieņemsim, ka masīvs ARR ar N elementiem atmiņā.
- Pirmajā solī tiek meklēta mazākā atslēga kopā ar tās pozīciju, tad ARR [POS] tiek nomainīts ar ARR [0]. Tāpēc ARR [0] ir sakārtots.
- Otrajā kārtā atkal mazākās vērtības pozīcija tiek noteikta N-1 elementu apakšgrupā. Apmainiet ARR [POS] ar ARR [1].
- N-1 caurlaidē notiek tāds pats process, lai kārtotu N elementu skaitu.
Piemērs :
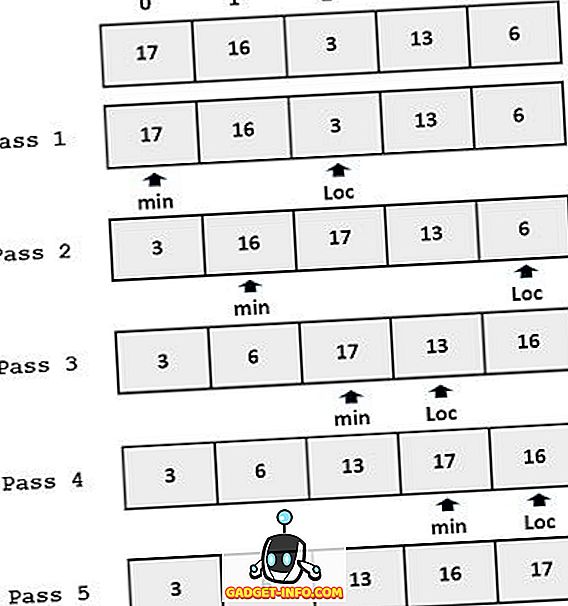
Galvenās atšķirības starp ievietošanas kārtību un atlasi Kārtot
- Ievietošanas kārtība parasti veic ievietošanas darbību. Gluži pretēji, atlases kārtība veic vajadzīgo elementu izvēli un izvietojumu.
- Tiek apgalvots, ka ievietošanas kārtība ir stabila, bet atlases kārtība nav stabils algoritms.
- Ievietošanas šķirošanas algoritmā elementi ir iepriekš zināmi. Turpretī atlases kārtībā ir atrašanās vieta iepriekš.
- Ievietošanas kārtošana ir tieša šķirošanas metode, kurā sarakstā esošie elementi tiek nekavējoties sakārtoti, bet atlases kārtība nevar darboties labi ar tūlītējiem datiem.
- Ievietošanas kārtībai vislabākajā gadījumā ir O (n) darbības laiks. Pretstatā labākajam atlases kārtas sarežģītības gadījumam ir O (n2).
Ievietošanas sarežģītība
Labākā ievietošanas veida sarežģītība ir O (n) reizes, ti, ja masīvs ir iepriekš sakārtots. Tādā pašā veidā, ja masīvs ir sakārtots apgrieztā secībā, pirmais nešķirotā masīva elements ir jāsalīdzina ar katru sakārtotā komplekta elementu. Tātad, sliktākajā gadījumā, ielikšanas veida darbības laiks ir kvadrātiskais, ti, O (n2) . Vidējā gadījumā tam ir arī jāsamazina minimālais (k-1) / 2 salīdzinājums. Līdz ar to vidējam gadījumam ir arī kvadrātiskais darbības laiks O (n2).
Atlases sarežģītība
Tā kā atlases, šķirošanas darbs nav atkarīgs no masīva elementu sākotnējās kārtības, tāpēc nav lielas atšķirības starp labāko gadījumu un sliktākā atlases veida sarežģītību.
Atlases kārtība atlasa minimālo vērtību elementu, atlases procesā tiek skenēts visu elementu skaits n; līdz ar to n-1 salīdzinājumi ir izdarīti pirmajā posmā. Tad elementi tiek savstarpēji aizstāti. Tāpat arī otrajā caurlaidē, lai atrastu otro mazāko elementu, nepieciešams skenēt pārējos n-1 elementus, un process tiek turpināts, līdz viss masīvs sakārtots.
Tādējādi atlases kārtas izpildes laika sarežģītība ir O (n2) .
= (n-1) + (n-2) + ……… .. + 2 + 1
= n (n-1) / 2 = O (n2)
Secinājums
No abiem šķirošanas algoritmiem ievietošanas kārtība ir ātra, efektīva, stabila, bet atlases kārtība darbojas efektīvi tikai tad, ja ir iesaistīts neliels elementu kopums vai saraksts ir daļēji iepriekš sakārtots. Salīdzinājumu skaits, kas izdarīts, atlasot šķirošanu, ir lielāks par veiktajām kustībām, bet ievietošanas kārtībā elementu pārvietošanas vai maiņas reižu skaits ir lielāks nekā izdarītie salīdzinājumi.