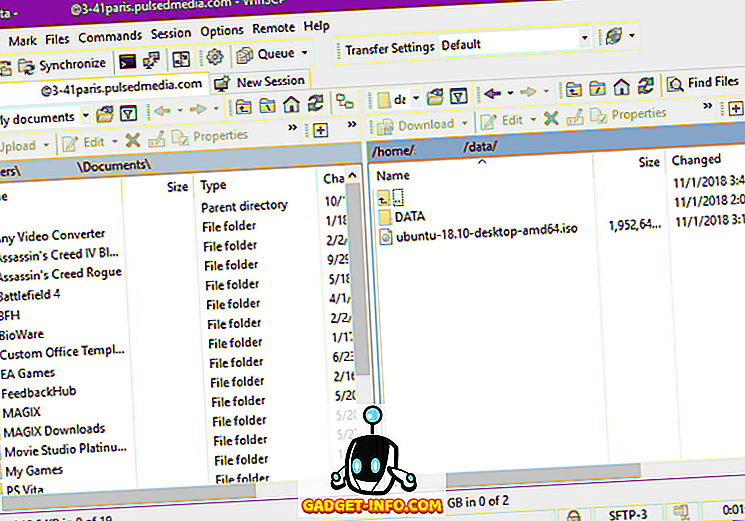
Atšķirībā no standarta novirzes ir skaitliskās vērtības kvadrātsakne, kas iegūta, aprēķinot dispersiju. Daudzi cilvēki kontrastē šīs divas matemātiskās koncepcijas. Tātad, šajā rakstā mēģināts apgaismot svarīgo atšķirību starp dispersiju un standarta novirzi.
Salīdzinājuma diagramma
| Salīdzinājuma pamats | Variants | Standarta novirze |
|---|---|---|
| Nozīme | Variancija ir skaitliska vērtība, kas apraksta novērojumu mainīgumu no tā vidējā aritmētiskā. | Standarta novirze ir novērojumu sadalījuma rādītājs datu kopā. |
| Kas tas ir? | Tā ir vidējā kvadrātu novirze. | Tā ir vidējā kvadrātiskā novirze. |
| Marķēts kā | Sigma-kvadrāts (σ ^ 2) | Sigma (σ) |
| Izteikta | Kvadrātu vienības | Tādas pašas vienības kā datu kopas vērtības. |
| Norāda | Cik tālu indivīdi grupā ir izkliedēti. | Cik daudz datu kopas novērojumi atšķiras no tā vidējā rādītāja. |
Variancijas definīcija
Statistikā dispersiju definē kā mainīguma lielumu, kas atspoguļo, cik tālu grupas dalībnieki ir sadalīti. Tā atklāj vidējo pakāpi, kādā katrs novērojums atšķiras no vidējā līmeņa. Ja datu kopas dispersija ir neliela, tas parāda datu punktu tuvumu vidējam rādītājam, bet lielāka dispersijas vērtība norāda, ka novērojumi ir ļoti izkliedēti ap aritmētisko vidējo un viens no otra.
Neklasificētiem datiem :
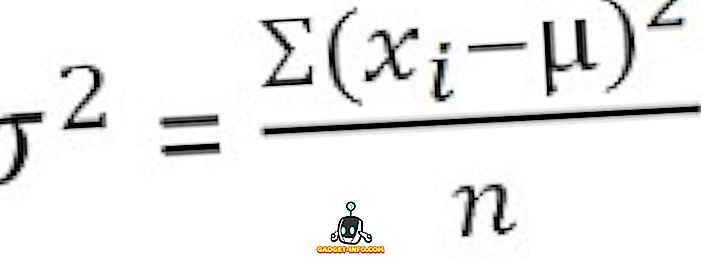
Grupētu frekvenču sadalījumam :
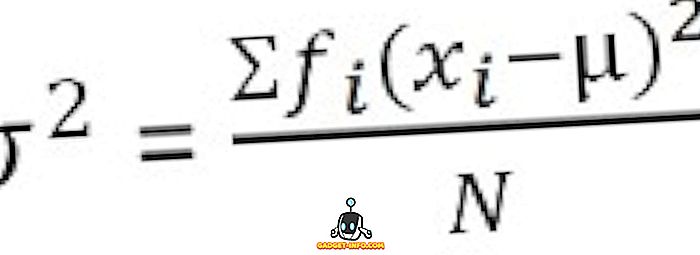
Standarta novirzes definīcija
Standarta novirze ir pasākums, kas kvantitatīvi nosaka novērojumu izkliedi datu kopā. Zema standarta novirze ir rādītāju tuvuma rādītājs aritmētiskajam vidējam lielumam un augsta standarta novirze; rādītāji ir izkliedēti augstākā vērtību diapazonā.
Neklasificētiem datiem :

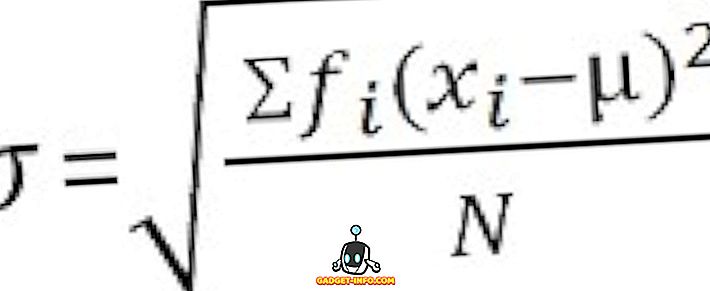
Galvenās atšķirības starp novirzi un standarta novirzi
Starpību starp standarta novirzi un dispersiju var skaidri noteikt, pamatojoties uz šādiem iemesliem:
- Variancija ir skaitliska vērtība, kas apraksta novērojumu mainīgumu no tā vidējā aritmētiskā. Standarta novirze ir novērojumu sadalījuma rādītājs datu kopā.
- Variancija ir nekas cits kā kvadrātu noviržu vidējais lielums. No otras puses, standarta novirze ir vidējā kvadrātiskā novirze.
- Varianci apzīmē ar sigma kvadrātu (σ2), bet standarta novirze ir apzīmēta kā sigma (σ).
- Variansi tiek izteikta kvadrātveida vienībās, kas parasti ir lielākas par dotā datu kopas vērtībām. Atšķirībā no standarta novirzes, kas izteikta vienādās vienībās kā datu kopas vērtības.
- Variancija nosaka, cik lielā mērā indivīdi grupā ir izkliedēti. Un otrādi, standarta novirze nosaka, cik daudz datu kopas novērojumu atšķiras no tā vidējā.
Attēls
Studenti ieguvuši atzīmes piecos mācību priekšmetos attiecīgi 60, 75, 46, 58 un 80. Jums ir jāzina standarta novirze un dispersija.
Pirmkārt, jums ir jāatrod vidējais rādītājs,

Tātad vidējās (vidējās) atzīmes ir 63, 8
Tagad aprēķiniet dispersiju
| X | A | (xA) | (XA) ^ 2 |
|---|---|---|---|
| 60 | 63.8 | -3, 8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17.8 | 316, 84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262, 44 |
Kur, X = novērojumi
A = vidējais aritmētiskais
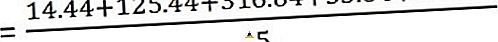
Un standarta novirze ir -

Līdzības
- Gan dispersijas, gan standarta novirzes vienmēr ir pozitīvas.
- Ja visi novērojumi datu kopā ir identiski, tad standarta novirze un dispersija būs nulle.
Secinājums
Šie divi ir galvenie statistikas termini, kuriem ir būtiska nozīme dažādās nozarēs. Standarta novirze ir labāka par vidējo, jo to izsaka tādās pašās vienībās kā mērījumu vienības, bet dispersiju izsaka vienībās, kas ir lielākas par doto datu kopu.