Saistībā ar šo, apvienojuma gadījumā rīkojums nav svarīgs. Ne tikai matemātikā, bet arī praktiskajā dzīvē, mēs regulāri ejam ar šiem diviem jēdzieniem. Lai gan mēs to nekad nepamanām. Tātad, uzmanīgi izlasiet rakstu, lai uzzinātu, kā šie divi jēdzieni ir atšķirīgi.
Salīdzinājuma diagramma
| Salīdzinājuma pamats | Permutācija | Kombinācija |
|---|---|---|
| Nozīme | Permutācija attiecas uz dažādiem veidiem, kā organizēt objektu kopumu secīgā secībā. | Kombinācija attiecas uz vairākiem veidiem, kā izvēlēties priekšmetus no liela objektu kopuma, tā ka to secība nav svarīga. |
| Pasūtījums | Attiecīgs | Nav nozīmes |
| Norāda | Vienošanās | Izvēle |
| Kas tas ir? | Pasūtītie elementi | Neregulēti komplekti |
| Atbildes | Cik daudz dažādu izkārtojumu var izveidot no konkrētu objektu kopas? | Cik daudz dažādu grupu var izvēlēties no lielākas objektu grupas? |
| Atvasināšana | Vairākas permutācijas no vienas kombinācijas. | Viena kombinācija no vienas permutācijas. |
Permutācijas definīcija
Mēs definējam permutāciju kā dažādus veidus, kā organizēt dažus vai visus komplekta dalībniekus noteiktā secībā. Tas nozīmē visu iespējamo konkrētā komplekta izvietojumu vai pārkārtošanu atšķirīgā secībā.
Piemēram, visas iespējamās permutācijas, kas izveidotas ar burtiem x, y, z -
- Veicot visus trīs vienlaicīgi, ir xyz, xzy, yxz, yzx, zxy, zyx.
- Uzņemot divas reizes, ir xy, xz, yx, yz, zx, zy.
Kopējo iespējamo n lietu permutāciju skaitu, kas ņemti r laikā, var aprēķināt kā:
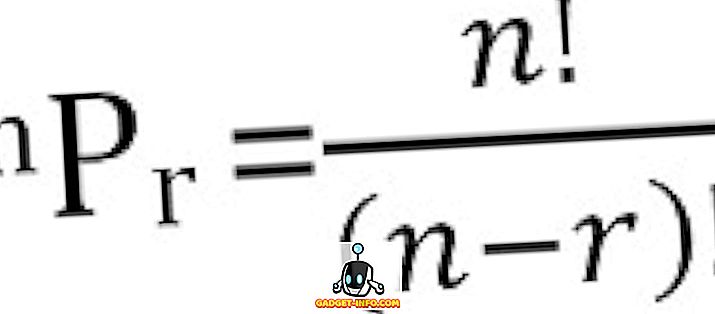
Kombinācijas definīcija
Kombinācija ir definēta kā dažādi veidi, izvēloties grupu, ņemot dažus vai visus kopas dalībniekus bez šāda secības.
Piemēram, visas iespējamās kombinācijas, kas izvēlētas ar burtu m, n, o -
- Izvēloties trīs no trim burtiem, vienīgā kombinācija ir mno
- Ja jāizvēlas divi no trim burtiem, tad iespējamās kombinācijas ir mn, no, om.
Kopējo iespējamo n kombināciju skaitu, kas ņemti r laikā, var aprēķināt kā:
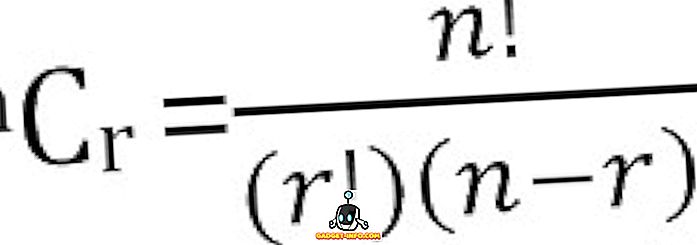
Galvenās atšķirības starp Permutācija un Kombināciju
Atšķirības starp permutāciju un kombināciju ir skaidri norādītas šādu iemeslu dēļ:
- Termins permutācija attiecas uz vairākiem veidiem, kā sakārtot objektu kopumu secīgā secībā. Kombinācija nozīmē vairākus veidus, kā izvēlēties priekšmetus no liela objektu kopuma, tāpēc to secība nav būtiska.
- Galvenais atšķirības punkts starp šiem diviem matemātiskajiem jēdzieniem ir kārtība, izvietojums un stāvoklis, ti, iepriekšminētajās permutācijas īpašībās ir nozīme, kas nav svarīga kombinācijas gadījumā.
- Permutācija apzīmē vairākus veidus, kā sakārtot lietas, cilvēkus, ciparus, alfabētus, krāsas utt. No otras puses, kombinācija norāda dažādus veidus, kā izvēlēties izvēlnes elementus, pārtiku, drēbes, priekšmetus utt.
- Permutācija ir nekas cits kā sakārtota kombinācija, bet kombinācija nozīmē neierobežotas kopas vai vērtību savienošanu konkrētos kritērijos.
- Daudzas permutācijas var iegūt no vienas kombinācijas. Savukārt tikai vienu kombināciju var iegūt no vienas permutācijas.
- Atbildes uz atbildēm Cik daudz dažādu režīmu var izveidot no konkrētā objektu kopuma? Atšķirībā no kombinācijas, kas izskaidro, cik dažādas grupas var izvēlēties no lielākas objektu grupas?
Piemērs
Pieņemsim, ka ir situācija, kad jums ir jāpārzina iespējamo divu iespējamo paraugu skaits no trim objektiem A, B, C. Šajā jautājumā vispirms ir jāsaprot, vai jautājums ir saistīts ar permutāciju vai kombinācija, un vienīgais veids, kā to uzzināt, ir pārbaudīt, vai pasūtījums ir svarīgs vai nē.
Ja rīkojums ir nozīmīgs, tad jautājums ir saistīts ar permutāciju, un iespējamie paraugi būs, AB, BA, BC, CB, AC, CA. Kur, AB atšķiras no BA, BC atšķiras no CB un AC ir atšķirīgs CA.
Ja rīkojums nav būtisks, jautājums ir saistīts ar kombināciju, un iespējamie paraugi būs AB, BC un CA.
Secinājums
Ar iepriekš minēto diskusiju ir skaidrs, ka permutācija un kombinācija ir dažādi termini, ko izmanto matemātikā, statistikā, pētniecībā un mūsu ikdienas dzīvē. Jāatceras, ka attiecībā uz šiem diviem jēdzieniem konkrētam objektu kopumam permutācija vienmēr būs lielāka nekā tās kombinācija.