Starpība starp vidējo un vidējo

• 2019

Centrālā tendence nozīmē datu punktu tendenci sasaistīt tās centrālo vai vidējo vērtību. Divi visbiežāk izmantotie centrālās tendences rādītāji ir vidēji un vidēji. Vidējais ir definēts kā dotā datu kopuma "centrālā" vērtība, bet vidējā vērtība ir "vidējā lielākā" vērtība dotajā datu kopā.

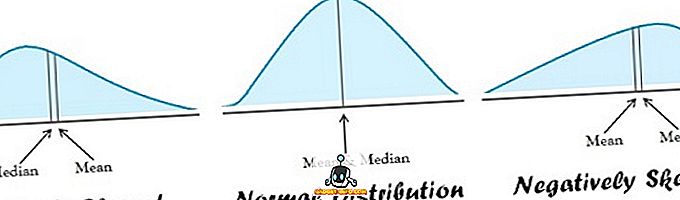
Ideāls centrālās tendences mērs ir tāds, kas ir skaidri definēts, viegli saprotams, vienkārši aprēķināms. Tam būtu jābalstās uz visiem novērojumiem un vismazāk jāietekmē ekstrēmie novērojumi, kas ir datu kopumā.

Cilvēki bieži pretstatīs šos divus pasākumus, bet fakts ir tāds, ka tie ir atšķirīgi. Šajā rakstā ir īpaši norādītas galvenās atšķirības starp vidējo un vidējo. Paskaties.

Salīdzinājuma diagramma

Salīdzinājuma pamats	Vidējais	Mediāna
Nozīme	Vidējā vērtība ir dotais vērtību vai daudzumu kopums.	Mediāns ir definēts kā vidējais numurs pasūtīto vērtību sarakstā.
Kas tas ir?	Tas ir vidējais aritmētiskais.	Tas ir pozicionālais vidējais rādītājs.
Pārstāv	Datu kopas smaguma centrs	Datu kopas smaguma centrs Datu kopas viduspunkts
Piemērojamība	Normāls sadalījums	Izkliedētais sadalījums
Izņēmumi	Vidējais ir jutīgs pret ārējiem rādītājiem.	Mediāna nav jutīga pret izņēmumiem.
Aprēķins	Vidējo aprēķina, pievienojot visus novērojumus un pēc tam dalot iegūto vērtību ar novērojumu skaitu.	Lai aprēķinātu vidējo vērtību, datu kopa ir sakārtota augošā vai dilstošā secībā, tad vērtība, kas atbilst jaunās datu kopas precīzai vidum, ir mediāna.

Mean definīcija

Vidējais ir plaši izmantots centrālās tendences mērs, kas definēts kā vērtību kopas vidējais rādītājs. Tas atspoguļo doto vērtību diapazona modeli un visbiežāko vērtību. To var aprēķināt gan atsevišķās, gan nepārtrauktās sērijās.

Vidējā vērtība ir vienāda ar visu novērojumu summu, kas dalīta ar novērojumu skaitu datu kopā. Ja mainīgā vērtība ir vienāda, tā vidējais rādītājs būs vienāds. Vidēji var būt divu veidu, parauga vidējais (x () un populācijas vidējais (µ). To var aprēķināt pēc formulas:

• Aritmētiskais vidējais : kur Ʃ = grieķu burts sigma, apzīmē “summu ..”
  n = vērtību skaits
• Diskrētām sērijām : kur, f = frekvence
• Nepārtrauktiem pakalpojumiem : kur d = (XA) / C
  A = Pieņemtais vidējais
  C = Kopējais dalītājs

Mediāna definīcija

Mediāna ir vēl viens svarīgs centrālās tendences rādītājs, ko izmanto, lai sadalītu vērtību divās vienādās daļās, ti, lielāku pusi no parauga, populācijas vai varbūtības sadalījuma no apakšējās puses. Tā ir vidējā vērtība, kas tiek sasniegta, kad novērojumi ir sakārtoti noteiktā secībā, augošā vai dilstošā secībā.

Lai aprēķinātu mediānu, vispirms sakārtojiet novērojumus zemākajā līdz augstākajam vai augstākajam līdz zemākajam, pēc tam piemērojiet atbilstošo formulu, kā norādīts zemāk:

• Ja novērojumu skaits ir nepāra : kur n = novērojumu skaits
• Ja novērojumu skaits ir pat :
• Pastāvīgām sērijām : kur l = vidējās klases zemākā robeža
  c = iepriekšējās vidējās klases kumulatīvā frekvence
  f = vidējās klases biežums
  h = klases platums

Galvenās atšķirības starp vidējo un vidējo

Ievērojamās atšķirības starp vidējo un vidējo rādītāju ir norādītas šajā pantā:

1. Statistikā vidējais ir definēts kā doto vērtību vai daudzumu kopums. Mediāna tiek uzskatīta par vidējo numuru pasūtīto vērtību sarakstā.
2. Lai gan vidējais ir vidējais aritmētiskais, mediāna ir pozicionālais vidējais, būtībā datu kopas stāvoklis nosaka mediāna vērtību.
3. Vidēji iezīmē datu kopas smaguma centru, bet mediāna izceļ datu kopas vidējo vērtību.
4. Vidējā vērtība ir piemērota parasti izplatītiem datiem. No otras puses, mediāna ir labākā, ja datu sadalījums ir izliekts.
5. Vidējo lielumu lielā mērā ietekmē ekstrēmā vērtība, kas nav saistīta ar mediānu.
6. Vidējo aprēķina, pievienojot visus novērojumus un pēc tam dalot iegūto vērtību ar novērojumu skaitu; rezultāts ir vidējais. Atšķirībā no mediānas, datu kopa ir sakārtota augošā vai dilstošā secībā, tad vērtība, kas ir jaunā datu kopas vidējā vērtība, ir mediāna.

Piemērs

Atrodiet norādīto datu kopas vidējo un vidējo vērtību:
58, 26, 65, 34, 78, 44, 96
Risinājums: lai aprēķinātu vidējo, jums ir jāsadala novērojumu summa ar novērojumu skaitu,

Vidējais = 57, 28
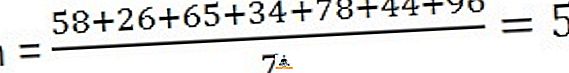
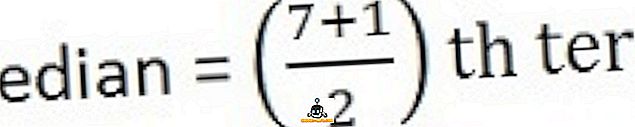
Lai aprēķinātu vidējo, vispirms sakārtot sēriju secībā, ti, zemākajā līdz augstākajai,
26, 34, 44, 58, 65, 78, 96

kur n = novērojumu skaits

Vidējā = 4. termiņš = 58

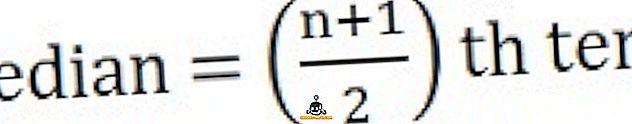
Secinājums

Pārskatot iepriekš minētos punktus, varam teikt, ka šie divi matemātiskie jēdzieni ir atšķirīgi. Aritmētisko vidējo vai vidējo rādītāju uzskata par labāko tendenci centrālajā tendencē, jo tajā ir visas ideāla pasākuma pazīmes, bet tam ir viens trūkums, ka paraugu ņemšanas svārstības ietekmē vidējo.

Tāpat arī mediāna ir nepārprotami definēta un viegli saprotama un aprēķināta, un vislabāk par šo pasākumu ir tas, ka to neietekmē paraugu ņemšanas svārstības, bet vienīgais mediāna trūkums ir tas, ka tas nav balstīts uz visiem novērojumus. Atvērta tipa klasifikācijai vidējā vērtība parasti ir lielāka par vidējo.