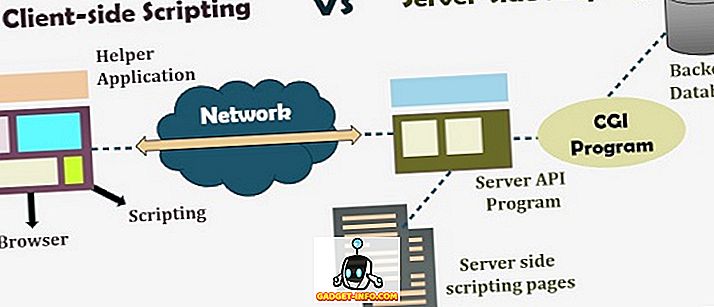
Teorētiskās varbūtības sadalījums ir definēts kā funkcija, kas katram iespējamam statistikas eksperimenta rezultātam piešķir varbūtību. Varbūtības sadalījums var būt diskrēts vai nepārtraukts, kur diskrētajā nejaušajā mainīgajā lielumā kopējā varbūtība tiek piešķirta dažādiem masas punktiem, bet nepārtrauktā nejaušā mainīgā varbūtība tiek sadalīta dažādos klasēs.
Binomālais sadalījums un Poisson sadalījums ir divi diskrēti varbūtības sadalījumi. Normāls sadalījums, studentu sadalījums, chi-kvadrātveida sadalījums un F sadalījums ir nepārtrauktas nejaušības mainīgā lieluma veidi. Tātad, šeit mēs ejam, lai apspriestu atšķirību starp Binoma un Poisson sadalījumu. Paskaties.
Salīdzinājuma diagramma
| Salīdzinājuma pamats | Binomālais sadalījums | Poisson Distribution |
|---|---|---|
| Nozīme | Binomālais sadalījums ir tāds, kurā tiek pētīta atkārtotu izmēģinājumu skaita iespējamība. | Poisson Distribution sniedz neatkarīgu notikumu skaitu, kas notiek nejauši ar noteiktu laika periodu. |
| Daba | Biparametrisks | Uniparametric |
| Izmēģinājumu skaits | Fiksētie | Bezgalīgs |
| Panākumi | Pastāvīga varbūtība | Bezgalīga panākumu iespēja |
| Rezultāti | Tikai divi iespējamie rezultāti, ti, panākumi vai neveiksmes. | Neierobežots skaits iespējamo rezultātu. |
| Vidējā un atšķirība | Vidējā> Dispersija | Vidējā = dispersija |
| Piemērs | Monētu tossing eksperiments. | Drukāšanas kļūdas / lielas grāmatas lapa. |
Binomālās izplatīšanas definīcija
Binomālais sadalījums ir plaši izmantotā varbūtības sadalījums, kas iegūts no Bernoulli procesa (nejaušs eksperiments, kas nosaukts pēc slavenā matemātiķa Bernulaļa). Tas ir pazīstams arī kā biparametriskais sadalījums, jo to raksturo divi parametri n un p. Šeit n ir atkārtoti pētījumi un p ir veiksmes varbūtība. Ja šo divu parametru vērtība ir zināma, tad tas nozīmē, ka sadalījums ir pilnībā zināms. Binomālā sadalījuma vidējais un dispersijas lielums ir apzīmēts ar µ = np un σ2 = npq.
P (X = x) = nC x px q n-x, x = 0, 1, 2, 3… n
= 0, pretējā gadījumā
Mēģinājumu radīt konkrētu rezultātu, kas nav zināms un nav iespējams, sauc par tiesu. Izmēģinājumi ir neatkarīgi un fiksēts pozitīvs vesels skaitlis. Tas ir saistīts ar diviem savstarpēji izslēdzošiem un izsmeļošiem notikumiem; kur notikums tiek saukts par panākumu un nevēlams, to sauc par neveiksmi. p ir veiksmes varbūtība, kamēr q = 1 - p ir kļūdas varbūtība, kas nemainās visā procesā.
Puasona izplatīšanas definīcija
1830. gadu beigās slavenais franču matemātiķis Simon Denis Poisson iepazīstināja ar šo izplatīšanu. Tajā aprakstīta iespēja, ka noteiktu notikumu skaits notiks noteiktā laika intervālā. Tas ir neparametrisks sadalījums, jo to parāda tikai viens parametrs λ vai m. Poisson sadalījuma vidējais lielums ir apzīmēts ar m, ti, µ = m vai λ un dispersiju apzīmē kā σ2 = m vai λ. X varbūtības masas funkciju attēlo:

Ja pasākuma skaits ir augsts, bet tās rašanās varbūtība ir samērā zema, tiek pielietota poissona izplatība. Piemēram, apdrošināšanas atlīdzību skaits dienā apdrošināšanas sabiedrībai.
Galvenās atšķirības starp binomisko un Poisson izplatīšanu
Atšķirības starp binomisko un poissona sadalījumu var izdarīt, pamatojoties uz šādiem iemesliem:
- Binomālais sadalījums ir tāds, kurā tiek pētīta atkārtotu izmēģinājumu skaita iespējamība. Varbūtības sadalījums, kas dod virkni neatkarīgu notikumu, notiek nejauši noteiktā laika periodā, to sauc par varbūtības sadalījumu.
- Binomālais sadalījums ir biparametrisks, ti, tas ir attēlots ar diviem parametriem n un p, bet Poisson sadalījums ir neparametrisks, ti, to raksturo viens parametrs m.
- Binomiālā izplatīšanā ir noteikts skaits mēģinājumu. No otras puses, neierobežots skaits izmēģinājumu ir poisson izplatījumā.
- Binomiskā sadalījuma panākumu varbūtība ir nemainīga, bet poisson izplatīšanā ir ļoti neliels panākumu skaits.
- Binomālā sadalījumā ir tikai divi iespējamie rezultāti, ti, panākumi vai neveiksmes. Pretēji tam, ir iespējama neierobežota skaita iespējamo rezultātu izpausmes gadījumā.
- Binomālā sadalījumā Vidējā> Variancija, kad Poisson sadalījuma vidējā = dispersija.
Secinājums
Neatkarīgi no iepriekš minētajām atšķirībām starp šiem diviem sadalījumiem ir vairāki līdzīgi aspekti, ti, abi ir diskrēta teorētiskā varbūtības sadalījums. Turklāt, pamatojoties uz parametru vērtībām, abas var būt unimodālas vai bimodālas. Turklāt binomisko sadalījumu var tuvināt ar Poisson sadalījumu, ja mēģinājumu skaits (n) mēdz būt bezgalīgs un veiksmes varbūtība (p) mēdz būt 0, lai m = np.