Atšķirība starp ANOVA un ANCOVA

2019

ANOVA ir efektīvs paņēmiens, lai veiktu pētījumus dažādās disciplīnās, piemēram, uzņēmējdarbībā, ekonomikā, psiholoģijā, bioloģijā un izglītībā, ja ir viens vai vairāki paraugi. Tas bieži tiek nepareizi interpretēts ar ANCOVA, jo abi tiek izmantoti, lai pārbaudītu atkarīgo mainīgo vidējo vērtību atšķirības, kas saistītas ar kontrolētiem neatkarīgiem mainīgajiem lielumiem, ņemot vērā nekontrolējamā neatkarīgā mainīgā sekas.

ANOVA izmanto, lai salīdzinātu un kontrastētu divu vai vairāku populāciju līdzekļus. ANCOVA izmanto, lai salīdzinātu vienu mainīgo divās vai vairākās populācijās, vienlaikus ņemot vērā citus mainīgos. Apskatiet rakstu, lai uzzinātu atšķirības starp ANOVA un ANCOVA.

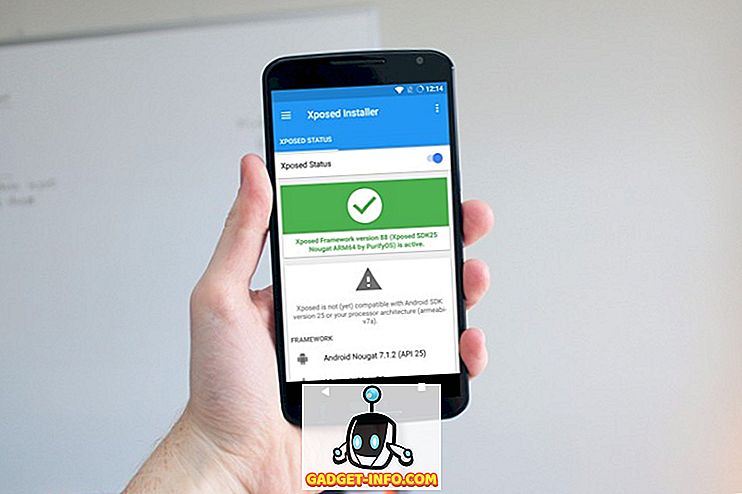
Salīdzinājuma diagramma

Salīdzinājuma pamats	ANOVA	ANCOVA
Nozīme	ANOVA ir process, kurā tiek pārbaudīta atšķirība starp vairāku datu grupu homogenitāti.	ANCOVA ir metode, kas novērš viena vai vairāku metriski skalotu nevēlamu mainīgo ietekmi no atkarīga mainīgā pirms pētījuma veikšanas.
Lietojumi	Tiek izmantots gan lineārs, gan nelineārs modelis.	Tiek izmantots tikai lineārs modelis.
Ietilpst	Kategorisks mainīgais.	Kategorijas un intervāla mainīgais.
Covariate	Ignorēts	Uzskata
BG variācija	Atšķirības starp grupas (BG) variāciju, ārstēšanu.	Sadalās starp grupas (BG) variāciju, ārstēšanu un kovariāciju.
WG variācija	Atribūti grupas ietvaros (WG) variācijas, individuālās atšķirības.	Sadalās grupas (WG) atšķirībās, atsevišķās atšķirībās un kovariātos.

ANOVA definīcija

ANOVA paplašinās līdz dispersijas analīzei, tiek aprakstīta kā statistikas metode, ko izmanto, lai noteiktu divu vai vairāku populāciju līdzekļu atšķirību, pārbaudot variāciju daudzumu paraugos, kas atbilst izmaiņu daudzumam starp paraugiem. Tas divkāršo datu kopas mainīgo summu divās daļās, ti, gadījumam piesaistītajai summai un konkrētiem iemesliem.

Tā ir metode, lai analizētu faktorus, kas ir hipotēzi vai ietekmē atkarīgo mainīgo. To var izmantot arī, lai izpētītu dažādo kategoriju atšķirības faktoros, kas sastāv no daudzām iespējamām vērtībām. Tas ir divu veidu:

Viens veids ANOVA : ja vienu faktoru izmanto, lai izpētītu atšķirību starp dažādām kategorijām, kam ir daudzas iespējamās vērtības.
Divvirzienu ANOVA : kad vienlaicīgi tiek pētīti divi faktori, lai izmērītu divu mainīgo vērtību ietekmējošo faktoru mijiedarbību.

ANCOVA definīcija

ANCOVA nozīmē "Covariance analīze", ir ANOVA paplašināta forma, kas novērš viena vai vairāku intervālu skalotu ārējo mainīgo ietekmi no atkarīgā mainīgā pirms pētījuma veikšanas. Tas ir viduspunkts starp ANOVA un regresijas analīzi, kur var salīdzināt vienu mainīgo lielumu divās vai vairākās populācijās, vienlaikus ņemot vērā citu mainīgo mainīgumu.

Neatkarīga mainīgā kopuma sastāvā ietilpst gan faktors (kategorisks neatkarīgais mainīgais), gan kovariāts (metriskais neatkarīgais mainīgais), izmantotā metode ir pazīstama kā ANCOVA. Atkarīgo mainīgo lielumu atšķirība kovariāta dēļ tiek atņemta, koriģējot atkarīgā mainīgā vidējo vērtību katrā ārstēšanas stāvoklī.

Šī metode ir piemērota, ja metriskais neatkarīgais mainīgais ir lineāri saistīts ar atkarīgo mainīgo, nevis citiem faktoriem. Tā pamatā ir daži pieņēmumi, kas ir:

Ir atkarība starp atkarīgo un nekontrolēto mainīgo.
Attiecības ir lineāras un ir identiskas no vienas grupas uz otru.
Dažādas ārstēšanas grupas tiek paņemtas pēc nejaušības principa.
Grupas mainīgums ir viendabīgs.

Galvenās atšķirības starp ANOVA un ANCOVA

Turpmāk minētie punkti ir būtiski, ciktāl tas attiecas uz atšķirību starp AOVA un ANCOVA:

Dažādo grupu homogenitātes noteikšanas varianta noteikšanas metode ir pazīstama kā dispersijas analīze vai ANOVA. Statistikas process, kas tiek izmantots, lai izslēgtu viena vai vairāku metriski mērogotu nevēlamu mainīgo ietekmi no atkarīga mainīgā pirms pētījuma veikšanas, ir pazīstams kā ANCOVA.
Lai gan ANOVA izmanto gan lineāru, gan nelineāru modeli. Gluži pretēji, ANCOVA izmanto tikai lineāru modeli.
ANOVA ietver tikai kategorisku neatkarīgu mainīgo, ti, faktoru. Pretēji tam ANCOVA ietver kategorisku un metrisku neatkarīgu mainīgo.
ANOVA nav ņemts vērā kovariāts, bet tas tiek ņemts vērā ANCOVA.
ANOVA raksturo starp grupas variācijām, tikai ārstēšanai. Turpretī ANCOVA dala grupas atšķirības pret ārstēšanu un kovariāciju.
ANOVA eksponē grupas atšķirības, īpaši individuālās atšķirības. Atšķirībā no ANCOVA, tas atšķiras grupas atšķirībās individuālajās atšķirībās un kovariātos.

Secinājums

Tādēļ, izmantojot iepriekš minēto diskusiju, jūs varētu būt skaidrs par atšķirībām starp abām statistikas metodēm. ANOVA izmanto, lai pārbaudītu divu grupu līdzekļus. No otras puses, ANCOVA ir progresīva analīzes analīze; kas apvieno gan ANOVA, gan regresijas analīzi.